近日，针对计算离散测度之间的最优传输问题，高性能计算部科研人员提出了一种多尺度稀疏Sinkhorn算法，改进了原来的多尺度Sinkhorn算法。通过统一计算设备架构（CUDA）实现并优化了该算法并应用于图片间的颜色传输。该研究成果被国际顶级会议IEEE Conference on Computer Vision and Pattern Recognition（CVPR，CCF A类）录用。论文第一作者为高性能部博士生陈逸东，导师为陆忠华研究员。 

　　最优传输用于表示两个分布的相似程度，在金融、统计、物理和机器学习等领域中具有十分重要作用。计算概率分布之间的最优传输在算法研究中具有非常高的热度。采用商业求解器Cplex求解器计算两张像素为256*256图片间的最优传输大约需要数个小时，消耗接近100GB内存。 

　　基于此，研究人员提出了一种在稀疏子集上迭代的算法，并提出了一种多尺度的方法来估计稀疏子集。研究人员证明了算法的收敛性，通过构造李雅普诺夫泛函，得到了所提算法收敛速率的上界估计。研究人员通过采用核函数截断法来计算子集，并首次给出了截断系数的上界，这是迄今理论上所获最佳结果。通过在CUDA上实现并优化该算法，使得计算256*256的图片之间最优传输的时间缩短到了3秒以内，显存消耗低于3GB；计算时间较商业求解器提升了1000倍以上，内存消耗减少了30倍。（撰稿：陈逸东） 

　　相关成果： 

　　Yidong Chen, Chen Li, Zhonghua Lu, Computing Wasserstein-p Distance Between Images with Linear Cost. IEEE Conference on Computer Vision and Pattern Recognition. 2022. 

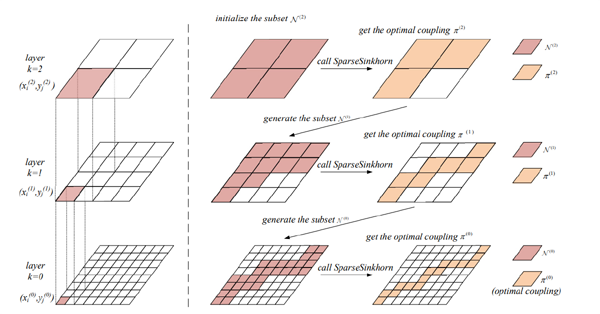
　　图1 采用多尺度方法估计子集 

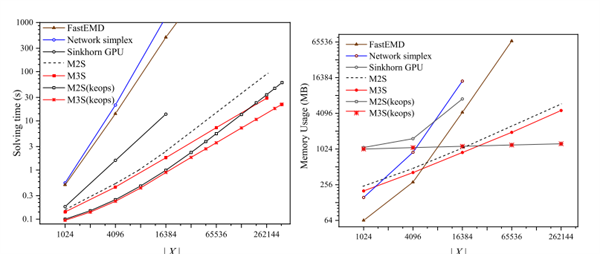
　　图2 不同求解器计算时间与消耗内存对比 

　　图3  1920*1200图片的最优传输与颜色传输计算